Next: Part 1: Continuous Time
Up: EEE 407/591 - Digital
Previous: Introduction
Main:
Main Lab Page
Introduction
The goal of this exercise is to examine the effects and use of sampling rate conversion and simulate a two-band QMF
(quadrature mirror filter) bank.
Problem 1: Up-Sampling/Down-Sampling
Description:
Use a signal generator for input. Set the input to a rectangular waveform of length 10 and
amplitude 1. Connect Sig. Gen. to a junction block. One output of the junction should be connected to a down-sampling block, that should be set to a rate of 2. The second output of
the junction, along with the output of the down-sampling block should now be connected to two FFT blocks. Finally connect the FFT block outputs to the inputs of a Plot2 block. Plot2 should now display the
spectra of the original and the down sampled signals.
- 1. Save the plot of spectra as graph1.
- 2. Change the down-sampling rate to 3 and note the change on the spectra and
save the plot as graph2.
- 3. Replace the down-sampling block with an up-sampling block of rate 2. Observe the
spectra and save as graph3. Also change the up-samplilng rate
to 3 and save the spectra as graph4.
- 4. For question 3, add
an interpolating filter at the output of the up-sampler. Design a lowpass Butterworth filter with cut-off frequency
pi/M, where M is the up-sampling rate
(consider M=3), 1 dB passband and 40 dB stopband, . Examine both the time and frequency domain signals before and after the filter.
Save the time and frequency domain of the signal before the filter as
graph5 and after the filter as graph6.
Problem 2: Design a fractional sampler
- 1. Design a sampler that will change the sampling rate of the input by a
fraction of 2/3. Consider the input signal to be rectangular pulse with
pulsewidth of 10. Include the necessary Butterworth filters with 1 dB
passband and 40 dB stopband. Save the block
diagram (in J-DSP) as graph7.
- 2. Save the time domain plot of the input (rectangular pulse) and
the output of the fractional sampler as graph8
- 3. Save the frequency responses of the filters as graph9. Is
it possible to use a single filter in this design?
Problem 3: Two-Band Filter Bank(QMF)
Description:
Go to the File menu at the top and select ‘new?to clear the workspace. Use
long signal generator (SigGen(L)) as the input. Connect it through a junction to two filter blocks. Connect the filter blocks to two down-sampling blocks and then to two up-sampling blocks
. Set the sampling rates to 2. The outputs of the up sampling blocks should now be connected to two more filters. The output of the two filters should be added together using an adder. As a last step connect the adder output to a Plot block. The system sh
ould look like this:
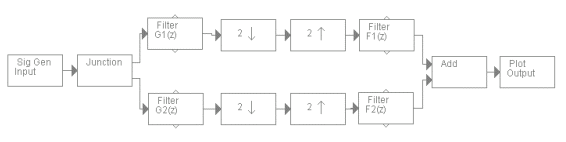
To set the filter coefficients, open the filter blocks and just type the coefficient values given below. When finished press enter or the ‘Update?button. After all filters have been set, look at the output signal.
Table-1: Nominal Filter coefficients:
| Filter | b0 | b1 |
|---|
| G1(z) | 0.5 | 0.5
|
|---|
| G2(z) | 0.5 | -0.5
|
|---|
| F1(z) | 1.0 | 1.0
|
|---|
| F2(z) | -1.0 | 1.0
|
|---|
Questions:
- 1.
Observe the output for Malespeaker-II as an input in long signal generator block
(SigGen(L)). Consider the 12th frame with frame size of 256 and 0% overlap. Save the both output and input as graph10.
- 2. Connect a frequency response block to the top output of each filter.
Observe their responses. How are they related? Save the frequency responses of G1(z) and G2(z) as graph11 and F1(z) and F2(z) as graph12.
Which filters are low pass filters and which are high pass filters?
- 3. How is the output of the filter bank different from the input signal?
Is it reconstructed perfectly?
- 4. In F2(z), change the parameters to b0 = 1 and b1 = -1 and check the effect on reconstructed
signal. Is it better or worse?
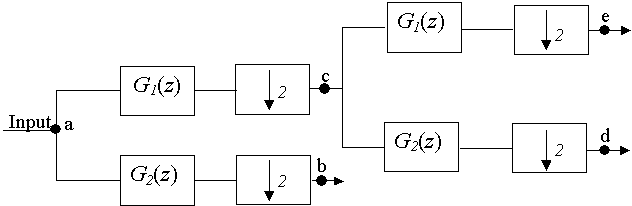
Problem 4: Tree Structured Subband
Realize the following block diagram in J-DSP. Use the coefficients as per
Table-1. Select the input as a sinc
function with pulsewidth 100. Check the signal spectra at the points a, b, c, d
and e and save those as graph13, graph14, graph15, graph16
and graph17.
Copyright 2002 Andreas Spanias, MIDL, Arizona State University
JDSP and Report Submission Software Developed by ASU-MIDL
For questions contact Prof. Spanias spanias@asu.edu.


